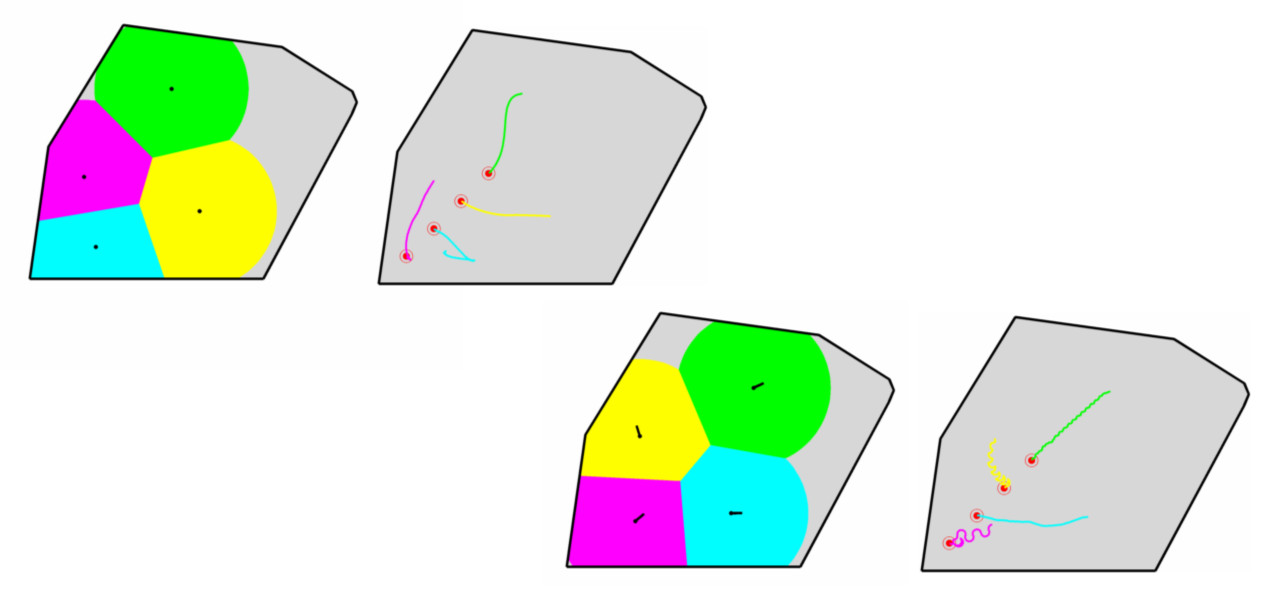
This is a project in the “Robotic Systems” course of the ECE department at the University of Patras, for the academic year 2011 - 2012. It involves controlling 4 mobile robots such that they cover the maximum area possible inside a polygon.
We are given a convex polygon with the following coordinates:
xa = [0 2.125 2.9325 2.975 2.9325 2.295 0.85 0.17];
ya = [0 0 1.5 1.6 1.7 2.1 2.3 1.2];
Inside this polygon, there are 4 mobile robots with the following initial positions and orientations:
xr = [0.25 0.5 0.75 1.0];
yr = [0.25 0.5 0.75 1.0];
th = [0 pi/6 pi/3 pi/2];The task is to simulate the trajectories of the robots as they coordinate in order to cover the maximum area of the polygon. Each robot is responsible for circular areas around it with the following radii:
R = [0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0];r-limited Voronoi cells are used for the estimation of the coverage area of each robot. There are two distinct modes of operation for the robots. In one mode, the robots hasve a skid-steer model, so they are free to move in any direction, effectively ignoring their orientation. In the second one, they have a car-like model (with \(\Delta\phi_{max}=15^o\)), constraining this way their controllability.
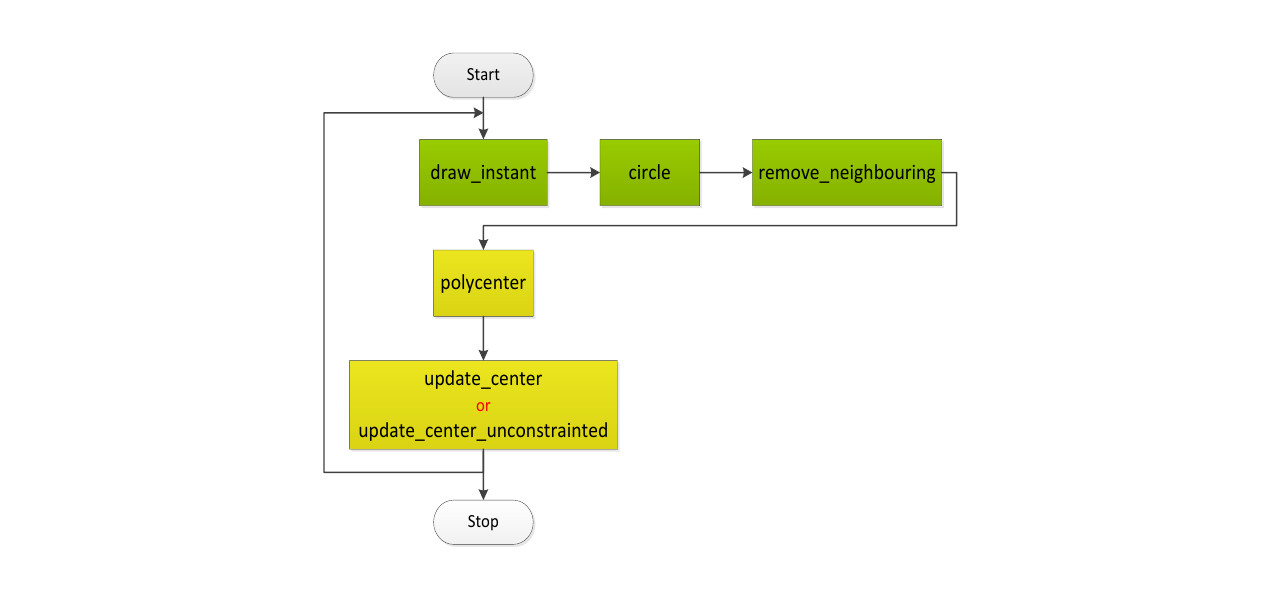
The r-limited Voronoi cell are estimated as follows:
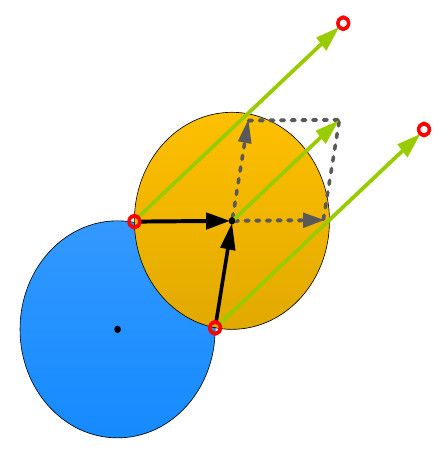
- We find the \(2\) potential points (red circles in the figure) where a Voronoi cell intersects a neighboring one. We calculate the vectors from these points to the center of the neighboring cell, and then we add these vectors to get a new one. This last vector will be perpendicular to the line connecting the intersecting points and will be pointing away from the center of the first cell. We extend this vector and add it to the intersecting points to get a new set of points, further away from the neighboring cell. Considering these \(4\) points, we have created a rectangular area that encloses the intersection of the two cells.
- We remove from the first cell the intersection between the cell and the computed rectangle, and we end up with a polygon that does not intersect the neighboring cell.
- We repeat the above steps for all neighboring cells.
- Finally, the r-limited Voronoi cell will be the intersection of the resulting polygon from the earlier steps with the convex hull of interest.
For the control input, we calculate the centroid of the r-limited Voronoi cell of each robot, and then we take a step towards these centroids while considering the modes of operation mentioned before.
The source code is available on GitHub.